Pytorch Functions You Should Know, Before Building Transformer
Basic Things you should know, Before you build Transformer Network from scratch.
1. TORCH.TENSOR
A PyTorch tensor is basically same as NumPy array.We can create/Construct a tensor using “torch.tensor()”
1
2
3
4
5
6
7
import torch
data = [1,2,3,4,5,6] #
my_tensor = torch.tensor(data)
print(f"Type : {type(my_tensor)}\nValue : {my_tensor}")
> Type : <class 'torch.Tensor'>
> Value : tensor([1, 2, 3, 4, 5, 6])
2. TORCH.TRIU
torch.triu can be used to create your masking matrix, It returns the upper triangular part of a matrix (2-D tensor) or batch of matrices, the other elements of the result tensor are set to 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
matrix = torch.arange(64).view(8,8)
triu_tensor = torch.triu(matrix)
print(triu_tensor)
> tensor([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 0, 9, 10, 11, 12, 13, 14, 15],
[ 0, 0, 18, 19, 20, 21, 22, 23],
[ 0, 0, 0, 27, 28, 29, 30, 31],
[ 0, 0, 0, 0, 36, 37, 38, 39],
[ 0, 0, 0, 0, 0, 45, 46, 47],
[ 0, 0, 0, 0, 0, 0, 54, 55],
[ 0, 0, 0, 0, 0, 0, 0, 63]])
3. TORCH.ADD
PyTorch torch.add() method adds a value to each element of the input tensor and returns a new modified tensor.
1
2
3
4
5
6
7
8
import torch
matrix1 = torch.tensor([[1,2],[1,2]])
matrix2 = torch.tensor([[2,4],[1,2]])
print(torch.add(matrix1,matrix2))
> tensor([[3, 6],
[2, 4]])
When you give input tensor and output tensor to “torch.add”, It returns the elementwise summed output.
4. TORCH.SUM
It returns the sum of all elments in tensor.
1
2
3
4
5
import torch
matrix1 = torch.tensor([[1,2],[1,2]])
print(torch.sum(matrix1))
> tensor(6)
5. TORCH.MM
It performs a matrix multiplication of the matrices(matrix1,matrix2)
1
2
3
4
5
6
7
import torch
matrix1 = torch.tensor([[1,2],[1,2]])
matrix2 = torch.tensor([[2,4],[1,2]])
print(torch.mm(matrix1,matrix2))
> tensor([[4, 8],
[4, 8]])
Note : “torch.mm” - performs a matrix multiplication without broadcasting - (2D tensor) by (2D tensor).
6. TORCH.MUL
Multiply input by other elementwise. 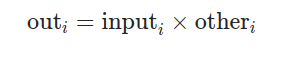
1
2
3
4
5
6
7
import torch
matrix1 = torch.tensor([[1,2],[1,2]])
matrix2 = torch.tensor([[2,4],[1,2]])
print(torch.mul(matrix1,matrix2))
> tensor([[2, 8],
[1, 4]])
Note : “torch.mul” - performs a elementwise multiplication with broadcasting - (Tensor) by (Tensor or Number)
7. TORCH.MATMUL
Matrix product of two tensors.
1
2
3
4
5
6
7
import torch
matrix1 = torch.tensor([[1,2],[1,2]])
matrix2 = torch.tensor([[2,4],[1,2]])
print(torch.matmul(matrix1,matrix2))
> tensor([[4, 8],
[4, 8]])
Note : “torch.matmul” - matrix product with broadcasting - (Tensor) by (Tensor) with different behaviors depending on the tensor shapes (dot product, matrix product, batched matrix products).
8. TORCH.CAT
Concatenates the given sequence of seq tensors in the given dimension. All tensors must have the same shape in the concatenating dimension.
“torch.cat” takes argument “dim”, The dimension over which the tensors are concatenated.(dim = 0 or dim = 1) default = 0.
1
2
3
4
5
6
7
8
9
import torch
matrix1 = torch.tensor([[1,2],[1,2]]) # (2,2)
matrix2 = torch.tensor([[2,4],[1,2]]) # (2,2)
print(torch.cat((matrix1,matrix2),dim = 0))
> tensor([[1, 2],
[1, 2],
[2, 4],
[1, 2]])
9. TORCH.STACK
It concatenates a sequence of tensors along a new dimension.
_All tensors need to be of the same size.
1
2
3
4
5
6
7
8
9
10
import torch
matrix1 = torch.tensor([[1,2],[1,2]]) # (2,2)
matrix2 = torch.tensor([[2,4],[1,2]]) # (2,2)
torch.stack((matrix1,matrix2),dim = 0)
> tensor([[[1, 2],
[1, 2]],
[[2, 4],
[1, 2]]])
10. TORCH.ZEROS_LIKE
Returns a tensor filled with the scalar value 0, with the same size as input.
“torch.zeros_like()” is equivalent to “torch.zeros()”
1
2
3
4
5
6
import torch
matrix = torch.tensor([[1,2],[1,2]]) # (2,2)
print(torch.zeros_like(matrix))
> tensor([[0, 0],
[0, 0]])
Advanced Things you should know, Before you build Transformer Network from scratch.
1. TORCH.BMM
Batchwise matrix multiplication,
matrix1 and matrix2 must be 3-D tensors each containing the same number of matrices.
If matrix1 is a (b×n×m) tensor, matrix2 is a (b×m×p) tensor, out will be a (b×n×p) tensor.
1
2
3
4
5
6
7
matrix1 = torch.tensor([[[1,2,3],[1,2,3]]]) # shape = (1,2,3) (b x n x m)
matrix2 = torch.tensor([[[1,2],[1,2],[1,2]]]) # shape = (1,3,2) (b x m x p)
print(torch.bmm(matrix1,matrix2)) # shape = (1,2,2) (b x n x p)
> tensor([[[ 6, 12],
[ 6, 12]]])
2. TORCH.MASKED_FILL
Fills the elements, Where mask is True.
1
2
3
4
5
6
7
8
9
10
import torch
mask = torch.arange(1,26).view(5,5).triu().bool() # upper triangle will be set to True
matrix1 = torch.arange(1,26).view(5,5)
print(torch.masked_fill(matrix1,mask = mask,value = 0)) # upper triangle True will be sent to 0
> tensor([[ 0, 0, 0, 0, 0],
[ 6, 0, 0, 0, 0],
[11, 12, 0, 0, 0],
[16, 17, 18, 0, 0],
[21, 22, 23, 24, 0]])
3. TORCH.ADDMM
Performs a matrix multiplication of the matrices matrix1 and matrix2. The matrix3 is added to the final result.
If matrix1 is a (n×m) tensor, matrix2 is a (m×p) tensor, then input must be broadcastable with a (n×p) tensor and output will be a (n×p) tensor.
1
2
3
4
5
6
7
8
9
10
11
import torch
matrix1 = torch.arange(1,16).view(5,3)
matrix2 = torch.arange(1,16).view(3,5)
matrix3 = torch.arange(1,26).view(5,5)
print(torch.addmm(matrix3,matrix1,matrix2)) # similar to torch.matmul(matrix1,matrix2).add(matrix3)
> tensor([[ 47, 54, 61, 68, 75],
[106, 122, 138, 154, 170],
[165, 190, 215, 240, 265],
[224, 258, 292, 326, 360],
[283, 326, 369, 412, 455]])
4. TORCH.BADDBMM
Performs a batchwise multiplication of matrices in batch1 and batch2. matrix3 is added to the final result.
Rule : batch1 and batch2 must be 3-D tensors each containing the same number of matrices.
1
2
3
4
5
6
7
8
import torch
batch1 = torch.tensor([[[1,2,3],[1,2,3]]]) # shape = (1,2,3) (b x n x m)
batch2 = torch.tensor([[[1,2],[1,2],[1,2]]]) # shape = (1,3,2) (b x m x p)
matrix3 = torch.tensor([[1,2],[1,2]])
print(torch.baddbmm(matrix3,batch1,batch2)) # similar to torch.bmm(batch1,batch2).add(matrix3)
> tensor([[[ 7, 14],
[ 7, 14]]])
5. TORCH.TENSOR.EXPAND
It returns a new view of the tensor with dimensions expanded to a larger size.
Tensor can be also expanded to a larger number of dimensions, and the new ones will be appended at the front. For the new dimensions, the size cannot be set to -1.
expand() will never allocate new memory. And so require the expanded dimension to be of size 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
matrix = torch.tensor([[1], [2], [3]]) # shape = (3,1)
print(matrix.expand(3,4))
> tensor([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
print(matrix.expand(-1,4)) # -1 means not changing the size of that dimension
> tensor([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
6. TORCH.TENSOR.REPEAT
Repeats this tensor along the specified dimensions.
Unlike expand(), this function copies the tensor’s data.
repeat() will always allocate new memory and the repeated dimension can be of any size.
1
2
3
4
5
6
7
import torch
matrix = torch.tensor([[1], [2], [3]]) # shape = (3,1)
print(matrix.repeat(1,4))
> tensor([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
Reference : Kaggle Notebook
